自動定理証明器 ACL2 の入門向けに L-99 の1問目を解きました
目次
1. 注意
この記事はいま思うとあまりよく分かっていなかったときに書いたものなので参考にしない方がいいです。 Lisp の説明のあたりは別に問題ないと思っていますが、実際に ACL2 に渡す補題を考えるときの心構え的な部分が微妙です。 近々、本当に役に立つ初心者向けの記事を書く予定なので作成しだいここにリンクを張ります。
2. はじめに
今回は L-99: Ninety-Nine Lisp Problems の問題の一問目を ACL2 でやっていきます。 L-99 は P-99: Ninety-Nine Prolog Problems という Prolog の 99 問の問題が Lisp に翻訳されたものです。Lisp の入門に広く使われている問題集になっています(要出典)。
L-99 の1問目を ACL2 で解いてさらにその関数の性質を ACL2 で証明することによって、 簡単に ACL2 の紹介をしようと思います。 といっても、この記事でできるのはちょっと ACL2 がどんな感じなのかを説明できるくらいで、 ACL2 に本格的に始めることを考えるとこの記事では力不足です。 なので、ACL2 - ACL2-tutorial を一度通して読むことを強くおすすめします。
なお、本記事に問題の答えを掲載してしまうため自分で解きたい人は見ないようにしてください。
一応、 details タグを使って私の答えは隠しているのですが答えに至るための考え方などは隠してません。
3. 本文中のコードのライセンス
自明なプログラムなので実際には著作物として認められないと思うのですが、 何も書かないと自由に扱えないと解釈される可能性があるため念のためライセンスを明示します。
本記事中のコードは3条項BSDライセンスとします。
4. 解説動画
この記事だけ読んでもよく分からないかもしれないので、 この記事の内容について解説した動画を作成しました。 Lisp に触れたことのない方向けの解説も多少しているので必要な人は見てみてください。
5. ACL2 の導入方法
ACL2 Version 8.4 Installation Guide からインストールしてください。 ACL2 のインストールには Common Lisp の実行環境が必要です。 詳細は ACL2 Version 8.4 Installation Guide: Requirements を確認してください。
6. ACL2 のオンライン実行環境の紹介
ACL2 を試すのには Proof Pad: a web-based IDE for ACL2 がおすすめです。
デフォルトで強力なライブラリ(std/lists など)が入っているため、
ACL2 - ACL2-tutorial にある問題をやるには不向きなところがあるのですが、
とりあえず実行環境を持っていない人が試すのに良いと思います。
7. 問題 P01: Find the last box of a list.
リストの最後のコンスセルを求めよという問題です(問題文の box はこの記事ではコンスセルと呼ぶことにします)。
Common Lisp には last という同様の動作をする関数があるのですがこれを自分で作ってみようということみたいです。
元サイトの例示と同様に my-last という名前で定義します。
7.1. コンスセルとは
コンスセルとは cons という関数で作成されるオブジェクトです。
cons は (cons x y) のように二つの引数を取って対を作成します。
対とは二つの要素を含むオブジェクトです。
本記事ではこのオブジェクトのことを「コンスセル」と呼ぶことにします。
コンスセルから一番目を取り出す関数を car, 二番目を取り出す関数を cdr と言います。
この記事ではコンスセルの一番目を「car部」、二番目を「cdr部」と呼ぶことにします。
上記は、次の二つの等式が成立することを意味します。
(car (cons x y)) = x(cdr (cons x y)) = y
例としてcar部はシンボル a, cdr部はシンボル b のような場合について例示します。
(cons 'a 'b)
出力:
(A . B)
これを図示するとこんな感じです。
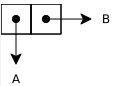
図1: (cons 'a 'b) のコンスセル
なおコンスセルはネストすることが可能であり、 コンスセルの要素がコンスセルであっても良いことに注意してください。
(cons (cons 'a 'b) (cons 'c 'd))
出力:
((A . B) C . D)
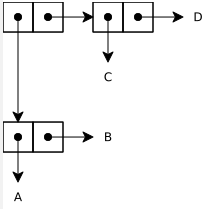
図2: (cons (cons 'a 'b) (cons 'c 'd)) のコンスセル
consp という関数を用いて、コンスセルかどうかを調べることができます。
ただし、実際には atom という関数を使うことの方が多いです。
atom はコンスセルでないことを調べる関数です。
次の等式が成立します。
(consp (cons x y)) = t(atom (cons x y)) = nil
なお、Lisp において nil は偽を意味します。
nil 以外の任意の値は真です。
しかし、明示的に真であることを強調したい場合には t を用います。
7.2. リストとは
- リストとは:
- シンボル
nilはリストである(この文脈ではnilを空リストという、'()と表記してもよい) - cdr 部がリストのコンスセルはリストである
- シンボル
2番目に注目してください。リストの定義の中にリストが入っています。
ただし、Common Lisp の listp 関数はコンスセルであるかシンボル
nil であるかしか確認調べてくれないことに注意してください。
上記の定義に照らすとリストの最後のコンスセルの cdr 部は nil である必要があるのですが、
listp 関数では最後に nil があるかどうかを調べてくれません。
Lisp 界隈では最後のコンスセルが nil でない場合もリストと呼ぶ場合があります、
なので最後のコンスセルのcdr部が nil であるような本当のリストであることを強調する「真リスト」という用語があります。
ACL2 には真リストかどうかを調べる true-listp という関数があります。
いくつか、リストの例示します。
(cons 'a (cons 'b (cons 'c (cons 'd nil))))
出力:
(A B C D)
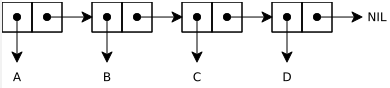
図3: (cons 'a (cons 'b (cons 'c (cons 'd nil)))) のリスト
7.3. my-last を定義する
この問題は再帰を用いて解きます。 理由は前述したとおり Lisp のリストが再帰的に定義されているからです。 再帰的な構造を扱う場合には再帰が適しています。
では、 my-last 関数を定義してみましょう。
次のように考えます。上から順番に条件分岐にしています。
- リストの最後のコンスセル
(my-last x)とは:xがコンスセルでない場合(atom)は解がない(最後のコンスセルは存在しない)- ACL2 の
last関数の挙動に合わせてxとします
- ACL2 の
xのcdr部がコンスセルでない場合:(atom (cdr x))- これが最後のコンスセルであるためそのまま
xです
- これが最後のコンスセルであるためそのまま
xのcdr部がコンスセルの場合(上記以外の場合):(and (consp x) (consp (cdr x)))xは最後のコンスセルではありません。 cdr部(先頭を除いた残りのリスト)の最後のコンスセルを求めます(my-last (cdr x))
上記の強調した部分が再帰的な部分です。
my-last の定義中に my-last を使います。
x がコンスセルでありかつそれが最後のコンスセルでないとき (my-last (cdr x)) が最後のコンスセルです。
今定義している my-last 関数はそもそも最後のコンスセルを求める関数であるためこのように定義できます。
しかし、これを聞いて「その理屈が成立するなら、 my-last 関数は最後のコンスセルを求める関数なのだから、このような条件分岐は書かずに単に最初から (my-last x) とだけ書けばよいではないか」と考えられるかもしれませんが、それでは駄目です。
関数の中で再帰的に関数を適用する場合、対象の値が 何らかの尺度で小さくなっていないとけません。
さもないと、 (my-last x) の値を求めようとした際に計算が停止し何らかの値を返すことを示すことができません。
ACL2 では関数の定義時に停止性の証明を行います。
停止性の証明に失敗した場合は関数の定義ができません。
(cdr x) は x と比べて「リストの長さ」という尺度で小さくなっています。
リストの長さは自然数(ここでは0を含むことにします、非負整数と同じ意味です)であり最小の値は0のため、
(cdr x) は x と比べてリストの長さが1減少することから必ずこの関数の再帰呼び出しはいずれ終わることが分かります。
ということで、次のように my-last 関数を定義します。
my-last には真リストじゃない値を入れてもよいこととします。
条件分岐には cond という構文を使用しています。
cond 構文の詳細について説明するのは面倒なので省略します。
P01 の解答: my-lastの定義
(defun my-last (x) (cond ((atom x) x) ((atom (cdr x)) x) (t (my-last (cdr x)))))
出力を確認する (11行)
The admission of MY-LAST is trivial, using the relation O< (which is known to be well-founded on the domain recognized by O-P) and the measure (ACL2-COUNT X). We observe that the type of MY-LAST is described by the theorem (OR (CONSP (MY-LAST X)) (EQUAL (MY-LAST X) X)). Summary Form: ( DEFUN MY-LAST ...) Rules: NIL Time: 0.01 seconds (prove: 0.00, print: 0.00, other: 0.01) MY-LAST
Lisper からの想定質問: 何故 null を使わないのか
基本的に基底部の判定に null を使うと関数の停止性の証明に失敗するからです(しかし、今回はたまたま null を使っても停止性の証明に成功します)。
ACL2 ではリストについて再帰するときの基底部の判定に null を使ってはいけません。
ACL2 の endp は ACL2 のガードという機能によって atom よりも強い制約がついているだけで実体は atom と同じです。
よって、 endp を使うのは適切ですがガードの説明をしていないため使っていません。
null を使うとコンスセルではない数字の 1 やシンボルの a などは、 nil ではないため、再帰部の方に入ります。その場合は停止性が証明できません。
ただし、今回の関数では atom を null で置き換えた場合 たまたま 停止性の証明に成功します。
何故かというと二個目の基底部の条件が (null (cdr x)) であり、
ACL2 では (cdr x) は x がコンスセルでない場合は nil
を返すことになっているので任意の値を与えても再帰部ではなくて基底部に入るので停止します。
ただ、偶然なのでこれに依存すべきではありません。
ACL2 ではリストの終端チェックには null ではなくて atom もしくは endp を使うと覚えておいてください(実際にはガードによって強い制約が付いているので基本的には endp を使った方が良いです)。
定義に成功しました。定義に成功すると下記のように出力されます。
The admission of MY-LAST is trivial, using the relation O< (which is known to be well-founded on the domain recognized by O-P) and the measure (ACL2-COUNT X). We observe that the type of MY-LAST is described by the theorem (OR (CONSP (MY-LAST X)) (EQUAL (MY-LAST X) X)). Summary Form: ( DEFUN MY-LAST ...) Rules: NIL Time: 0.00 seconds (prove: 0.00, print: 0.00, other: 0.00) MY-LAST
上記の出力をよく読むと分かるのですが、ACL2 は停止性の証明に使用する尺度として「リストの長さ」ではなくて、
汎用的な (acl2-count x) という式を使用しています。
これについては深く触れませんが「リストの長さ」が小さくなるときには (acl2-count x) の値も小さくなるように acl2-count が定義されているので問題にはなりません。
(acl2-count x) では不適な場合は尺度に使用する式を変更することができます。
また、 O-P のドメインでといった記述がありますがこれは順序数を意味しています。
順序数は片手間で説明できるような概念ではないので、とりあえずは順序を表わす数としての自然数を拡張した概念だと思っていてください。
アッカーマン関数のような複雑な関数の停止性を証明する場合に必要になります。
正しく動作しているかテストしてみましょう。
(my-last '(a b c d))
出力:
(D)
問題なさそうです。
8. my-last が正しく定義できているかを確認する (rev 編)
では、この my-last 関数が本当に最後のリストを参照しているかを確認しましょう。
まず、リストを反転する rev という関数を定義します。
この関数の中で使われている append はリストを連結する関数で、
list は与えた引数からなるリストを作成する関数です。
このリスト反転する関数の定義は定理証明の文脈では便利なのですが、
計算時の効率は非常に悪いので注意してください。
(defun rev (x) (if (atom x) nil (append (rev (cdr x)) (list (car x)))))
出力を確認する (14行)
The admission of REV is trivial, using the relation O< (which is known
to be well-founded on the domain recognized by O-P) and the measure
(ACL2-COUNT X). We observe that the type of REV is described by the
theorem (TRUE-LISTP (REV X)). We used primitive type reasoning and
the :type-prescription rules BINARY-APPEND and TRUE-LISTP-APPEND.
Summary
Form: ( DEFUN REV ...)
Rules: ((:FAKE-RUNE-FOR-TYPE-SET NIL)
(:TYPE-PRESCRIPTION BINARY-APPEND)
(:TYPE-PRESCRIPTION TRUE-LISTP-APPEND))
Time: 0.00 seconds (prove: 0.00, print: 0.00, other: 0.00)
REV
(rev '(a b c d))
出力:
(D C B A)
この結果の先頭とcar部と my-last のcar部は必ず一致します。
これを証明しましょう。
:rule-classes nil の意味については後で説明します。
(defthm car-my-last-equal-car-rev
(equal (car (my-last x)) (car (rev x)))
:rule-classes nil)
証明失敗: 出力を確認する (90行)
*1 (the initial Goal, a key checkpoint) is pushed for proof by induction.
Perhaps we can prove *1 by induction. Two induction schemes are suggested
by this conjecture. Subsumption reduces that number to one.
We will induct according to a scheme suggested by (MY-LAST X). This
suggestion was produced using the :induction rules MY-LAST and REV.
If we let (:P X) denote *1 above then the induction scheme we'll use
is
(AND (IMPLIES (AND (NOT (ATOM X))
(NOT (ATOM (CDR X)))
(:P (CDR X)))
(:P X))
(IMPLIES (AND (NOT (ATOM X)) (ATOM (CDR X)))
(:P X))
(IMPLIES (ATOM X) (:P X))).
This induction is justified by the same argument used to admit MY-LAST.
When applied to the goal at hand the above induction scheme produces
three nontautological subgoals.
Subgoal *1/3
Subgoal *1/3'
Subgoal *1/3''
Subgoal *1/3'''
Subgoal *1/3'4'
Subgoal *1/3'5'
Subgoal *1/3'6'
Subgoal *1/3.2
Subgoal *1/3.2'
Subgoal *1/3.2''
Subgoal *1/3.2'''
([ A key checkpoint while proving *1 (descended from Goal):
Subgoal *1/3''
(IMPLIES (AND (CONSP X)
(CONSP (CDR X))
(EQUAL (CAR (MY-LAST (CDR X)))
(CAR (REV (CDR X)))))
(EQUAL (CAR (MY-LAST (CDR X)))
(CAR (APPEND (REV (CDR X)) (LIST (CAR X))))))
A goal of NIL, Subgoal *1/3.2''', has been generated! Obviously, the
proof attempt has failed.
])
Summary
Form: ( DEFTHM CAR-MY-LAST-EQUAL-CAR-REV ...)
Rules: ((:DEFINITION ATOM)
(:DEFINITION BINARY-APPEND)
(:DEFINITION MY-LAST)
(:DEFINITION NOT)
(:DEFINITION REV)
(:DEFINITION TRUE-LISTP)
(:ELIM CAR-CDR-ELIM)
(:EXECUTABLE-COUNTERPART CAR)
(:EXECUTABLE-COUNTERPART CONSP)
(:FAKE-RUNE-FOR-TYPE-SET NIL)
(:INDUCTION MY-LAST)
(:INDUCTION REV)
(:REWRITE CAR-CONS)
(:TYPE-PRESCRIPTION REV))
Time: 0.01 seconds (prove: 0.01, print: 0.00, other: 0.00)
Prover steps counted: 1139
---
The key checkpoint goals, below, may help you to debug this failure.
See :DOC failure and see :DOC set-checkpoint-summary-limit.
---
*** Key checkpoint at the top level: ***
Goal
(EQUAL (CAR (MY-LAST X)) (CAR (REV X)))
*** Key checkpoint under a top-level induction
before generating a goal of NIL (see :DOC nil-goal): ***
Subgoal *1/3''
(IMPLIES (AND (CONSP X)
(CONSP (CDR X))
(EQUAL (CAR (MY-LAST (CDR X)))
(CAR (REV (CDR X)))))
(EQUAL (CAR (MY-LAST (CDR X)))
(CAR (APPEND (REV (CDR X)) (LIST (CAR X))))))
ACL2 Error in ( DEFTHM CAR-MY-LAST-EQUAL-CAR-REV ...): See :DOC failure.
******** FAILED ********
証明に失敗してしまいました。
なお、Proof Pad を使用している方はこの証明には失敗しないはずです。
なぜなら、 Proof Pad では最初から std/lists というライブラリが読み込まれており、
この定理の証明に必要な補助定理が既に定義されているからです。
同じ失敗を再現したい方は手元に ACL2 の環境を構築して試してみてください。
この定理の証明に失敗した原因を考えましょう。
証明に失敗したらとりあえず出力の最後のところに書いてある Subgoal *1/2.2 を読みます。
(IMPLIES (AND (CONSP X)
(CONSP (CDR X))
(EQUAL (CAR (MY-LAST (CDR X)))
(CAR (REV (CDR X)))))
(EQUAL (CAR (MY-LAST (CDR X)))
(CAR (APPEND (REV (CDR X)) (LIST (CAR X))))))
(car (append x y)) という構造があることに注目します。
(append x y) は x と y を連結したものです。
よく考えてみましょう。 (car (append x y)) は x がコンスセルだった場合は、
(car x) と同じです。そうでない場合は (append x y) は y なので (car y) と同じといえます。
このことを示す補助定理(厳密にはまだ予想ですが) car-append を定義してみましょう。
なお、 car-my-last-equal-car-rev と違って :rule-classes を省略していることに注意してください。
この場合、 :rule-classes :rewrite と指定されたことになります。
このように定義すると Rewrite ルールというものが作られ (equal x y) のような形をした定理であれば、
x を y に書き換えられることを ACL2 の Rewrite ルールのデータベースに登録しています(equal の中身の順番は大切です x と y を逆にしたら逆の意味になってしまいます)。
Rewrite ルールを ACL2 に追加したくない場合には明示的に :rule-classes nil と記載する必要があることに注意してください。
(defthm car-append
(equal (car (append x y))
(if (consp x)
(car x)
(car y))))
証明成功: 出力を確認する (16行)
Subgoal 2
Subgoal 2'
Subgoal 1
Q.E.D.
Summary
Form: ( DEFTHM CAR-APPEND ...)
Rules: ((:DEFINITION BINARY-APPEND)
(:ELIM CAR-CDR-ELIM)
(:FAKE-RUNE-FOR-TYPE-SET NIL)
(:REWRITE CAR-CONS)
(:REWRITE CDR-CONS))
Time: 0.00 seconds (prove: 0.00, print: 0.00, other: 0.00)
Prover steps counted: 204
CAR-APPEND
car-append の証明に成功しました。
Rewrite ルールとして登録したので今後 (car (append x y)) が出てきたら (if (consp x) (car x) (car y)) に書き換えられます。
再度 car-my-last-equal-car-rev 証明を試みましょう。
(defthm car-my-last-equal-car-rev
(equal (car (my-last x)) (car (rev x)))
:rule-classes nil)
証明成功: 出力を確認する (87行)
*1 (the initial Goal, a key checkpoint) is pushed for proof by induction.
Perhaps we can prove *1 by induction. Two induction schemes are suggested
by this conjecture. Subsumption reduces that number to one.
We will induct according to a scheme suggested by (MY-LAST X). This
suggestion was produced using the :induction rules MY-LAST and REV.
If we let (:P X) denote *1 above then the induction scheme we'll use
is
(AND (IMPLIES (AND (NOT (ATOM X))
(NOT (ATOM (CDR X)))
(:P (CDR X)))
(:P X))
(IMPLIES (AND (NOT (ATOM X)) (ATOM (CDR X)))
(:P X))
(IMPLIES (ATOM X) (:P X))).
This induction is justified by the same argument used to admit MY-LAST.
When applied to the goal at hand the above induction scheme produces
three nontautological subgoals.
Subgoal *1/3
Subgoal *1/3'
Subgoal *1/3''
Subgoal *1/3'''
Subgoal *1/3'4'
Subgoal *1/3'5'
Subgoal *1/3'6'
([ A key checkpoint while proving *1 (descended from Goal):
Subgoal *1/3'''
(IMPLIES (AND (CONSP X)
(CONSP (CDR X))
(NOT (CAR (MY-LAST (CDR X))))
(NOT (CONSP (REV (CDR X)))))
(NOT (CAR X)))
*1.1 (Subgoal *1/3'6') is pushed for proof by induction.
])
Subgoal *1/2
Subgoal *1/2'
Subgoal *1/2''
Subgoal *1/1
Subgoal *1/1'
So we now return to *1.1, which is
(IMPLIES (AND (CONSP X2)
(NOT (CAR (MY-LAST X2))))
(CONSP (REV X2))).
Subgoal *1.1/3
Subgoal *1.1/3'
Subgoal *1.1/2
Subgoal *1.1/2'
Subgoal *1.1/1
Subgoal *1.1/1'
*1.1 and *1 are COMPLETED!
Thus key checkpoints Subgoal *1/3''' and Goal are COMPLETED!
Q.E.D.
Summary
Form: ( DEFTHM CAR-MY-LAST-EQUAL-CAR-REV ...)
Rules: ((:DEFINITION ATOM)
(:DEFINITION MY-LAST)
(:DEFINITION NOT)
(:DEFINITION REV)
(:ELIM CAR-CDR-ELIM)
(:EXECUTABLE-COUNTERPART CAR)
(:EXECUTABLE-COUNTERPART CONS)
(:EXECUTABLE-COUNTERPART CONSP)
(:EXECUTABLE-COUNTERPART EQUAL)
(:EXECUTABLE-COUNTERPART TRUE-LISTP)
(:FAKE-RUNE-FOR-TYPE-SET NIL)
(:INDUCTION MY-LAST)
(:INDUCTION REV)
(:REWRITE CAR-APPEND)
(:REWRITE CAR-CONS)
(:REWRITE DEFAULT-CAR)
(:TYPE-PRESCRIPTION BINARY-APPEND)
(:TYPE-PRESCRIPTION REV)
(:TYPE-PRESCRIPTION TRUE-LISTP-APPEND))
Time: 0.01 seconds (prove: 0.00, print: 0.00, other: 0.00)
Prover steps counted: 1368
CAR-MY-LAST-EQUAL-CAR-REV
今度は定理の証明に成功しました。
8.1. ACL2 はどうやって定理を自動証明したのか
car-my-last-equal-car-rev の定理を ACL2 に与えたときの出力の下記の部分を見てください。
Perhaps we can prove *1 by induction. Two induction schemes are suggested
by this conjecture. Subsumption reduces that number to one.
We will induct according to a scheme suggested by (MY-LAST X). This
suggestion was produced using the :induction rules MY-LAST and REV.
If we let (:P X) denote *1 above then the induction scheme we'll use
is
(AND (IMPLIES (AND (NOT (ATOM X))
(NOT (ATOM (CDR X)))
(:P (CDR X)))
(:P X))
(IMPLIES (AND (NOT (ATOM X)) (ATOM (CDR X)))
(:P X))
(IMPLIES (ATOM X) (:P X))).
This induction is justified by the same argument used to admit MY-LAST.
When applied to the goal at hand the above induction scheme produces
three nontautological subgoals.
induction とは数学的帰納法のことです(以後、「帰納法」と略します)。
どのような帰納法を使うかは my-last 関数の定義から生成した式を用いています。
もしも ACL2 による帰納法の選択に間違いがある場合には、ヒントを与えることで指定できます。詳細は Induction を参照してください。
なお、関数の定義から帰納法の式を導く具体的な方法については、書籍 『定理証明手習い』に詳しく書かれているので ACL2 を使う前に読むことをおすすめします。
生成した帰納法の式を ACL2 の持っている書き換えルールのデータベースを用いて式を書き換えた結果が真になったため証明に成功したという感じです。 自動的にやられてしまっているのでよく分からないと思うのですが、これも 『定理証明手習い』 を読むことで手動で式を書き換えて定理証明をする体験をすれば何となく ACL2 が何をしているのかが分かると思います。
具体的にどんなステップを踏んだかについて調べる方法について私は知りません……。 ただ、下記の出力の最後にある通り証明完了まで 1368 ステップ踏んでいるようなので読めたとしても人間に簡単に理解できる内容ではないと思います。『定理証明手習い』を読んで満足し、ACL2 で証明に成功した場合は詳細について深く考えないことをおすすめします。
Time: 0.01 seconds (prove: 0.01, print: 0.00, other: 0.00) Prover steps counted: 1368 CAR-MY-LAST-EQUAL-CAR-REV
9. my-last が正しく定義できているかを確認する (nth 編)
ACL2 には nth という関数があります。
(nth i x) とすることでリスト x から0から数えて i 番目の要素を取り出すことができます。
(nth 3 '(a b c d e))
出力:
D
リストの長さを求める len という関数もあります。
(len '(a b c d e))
出力:
5
nth と len の両方を使うことで、リストの最後の要素を取り出せます。
(nth (- (len '(a b c d e)) 1) '(a b c d e))
出力:
E
同様に (car (my-last x)) にて最後の要素を取り出すことができます。
(car (my-last '(a b c d e)))
出力:
E
このことを定理にして証明してみましょう。
(defthm len-nth-car-my-last
(equal (nth (- (len x) 1) x)
(car (my-last x))))
証明成功: 出力を確認する (64行)
*1 (the initial Goal, a key checkpoint) is pushed for proof by induction.
Perhaps we can prove *1 by induction. Two induction schemes are suggested
by this conjecture. These merge into one derived induction scheme.
We will induct according to a scheme suggested by (MY-LAST X). This
suggestion was produced using the :induction rules LEN and MY-LAST.
If we let (:P X) denote *1 above then the induction scheme we'll use
is
(AND (IMPLIES (AND (NOT (ATOM X))
(NOT (ATOM (CDR X)))
(:P (CDR X)))
(:P X))
(IMPLIES (AND (NOT (ATOM X)) (ATOM (CDR X)))
(:P X))
(IMPLIES (ATOM X) (:P X))).
This induction is justified by the same argument used to admit MY-LAST.
When applied to the goal at hand the above induction scheme produces
three nontautological subgoals.
Subgoal *1/3
Subgoal *1/3'
Subgoal *1/3''
Subgoal *1/3'''
Subgoal *1/3'4'
Subgoal *1/3'5'
Subgoal *1/2
Subgoal *1/2'
Subgoal *1/2''
Subgoal *1/1
Subgoal *1/1'
*1 is COMPLETED!
Thus key checkpoint Goal is COMPLETED!
Q.E.D.
Summary
Form: ( DEFTHM LEN-NTH-CAR-MY-LAST ...)
Rules: ((:DEFINITION ATOM)
(:DEFINITION FIX)
(:DEFINITION LEN)
(:DEFINITION MY-LAST)
(:DEFINITION NOT)
(:DEFINITION NTH)
(:DEFINITION SYNP)
(:ELIM CAR-CDR-ELIM)
(:EXECUTABLE-COUNTERPART <)
(:EXECUTABLE-COUNTERPART BINARY-+)
(:EXECUTABLE-COUNTERPART EQUAL)
(:EXECUTABLE-COUNTERPART ZP)
(:FAKE-RUNE-FOR-LINEAR NIL)
(:FAKE-RUNE-FOR-TYPE-SET NIL)
(:INDUCTION LEN)
(:INDUCTION MY-LAST)
(:REWRITE CDR-CONS)
(:REWRITE DEFAULT-CAR)
(:REWRITE FOLD-CONSTS-IN-+)
(:REWRITE UNICITY-OF-0)
(:REWRITE ZP-OPEN)
(:TYPE-PRESCRIPTION LEN))
Time: 0.01 seconds (prove: 0.00, print: 0.00, other: 0.00)
Prover steps counted: 1147
LEN-NTH-CAR-MY-LAST
特に問題なく証明できました。
10. my-last が last と等しいことを証明
最後に my-last が ACL2 に定義されている last と同じものであることを証明します。
これを示す my-last-equal-last という定理を定義しましょう。
(defthm my-last-equal-last (equal (my-last x) (last x)))
証明成功: 出力を確認する (46行)
*1 (the initial Goal, a key checkpoint) is pushed for proof by induction.
Perhaps we can prove *1 by induction. Two induction schemes are suggested
by this conjecture. Subsumption reduces that number to one.
We will induct according to a scheme suggested by (MY-LAST X). This
suggestion was produced using the :induction rules LAST and MY-LAST.
If we let (:P X) denote *1 above then the induction scheme we'll use
is
(AND (IMPLIES (AND (NOT (ATOM X))
(NOT (ATOM (CDR X)))
(:P (CDR X)))
(:P X))
(IMPLIES (AND (NOT (ATOM X)) (ATOM (CDR X)))
(:P X))
(IMPLIES (ATOM X) (:P X))).
This induction is justified by the same argument used to admit MY-LAST.
When applied to the goal at hand the above induction scheme produces
three nontautological subgoals.
Subgoal *1/3
Subgoal *1/3'
Subgoal *1/2
Subgoal *1/2'
Subgoal *1/1
Subgoal *1/1'
*1 is COMPLETED!
Thus key checkpoint Goal is COMPLETED!
Q.E.D.
Summary
Form: ( DEFTHM MY-LAST-EQUAL-LAST ...)
Rules: ((:DEFINITION ATOM)
(:DEFINITION LAST)
(:DEFINITION MY-LAST)
(:DEFINITION NOT)
(:EXECUTABLE-COUNTERPART CONSP)
(:FAKE-RUNE-FOR-TYPE-SET NIL)
(:INDUCTION LAST)
(:INDUCTION MY-LAST)
(:REWRITE DEFAULT-CDR))
Time: 0.00 seconds (prove: 0.00, print: 0.00, other: 0.00)
Prover steps counted: 315
MY-LAST-EQUAL-LAST
証明に成功しました。
今後、 (my-last x) は (last x) に書き換えられるようになります。
11. おわりに
L-99 の1問目を通して ACL2 の基本的な使い方について解説しました。 この記事の内容だけでは実際には全然足りていないので、 ACL2-tutorial を読んで ACL2 の使い方について学んでから使ってみるのをおすすめします。 リンク先にも記載されていますが、残念ながら ACL2 は学んでから使わないとイライラして挫折する危険のある異様に学習曲線が急激なソフトウェアです。 なので、この記事を読んで ACL2 やってみよってする前に ACL2-tutorial をやることを強く推奨します。
また、L-99 についてはシリーズ化して不定期に記事を投稿していこうと考えています。
